| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 |
- Bellman Expectation Equation
- graph nueral network
- 그래프신경망
- Bellman Optimality Equation
- joint entropy
- 그래프뉴럴네트워크
- 벨만기대방정식
- Monte-calro
- conditional entropy
- 마르코프
- Bellman equation
- 강화학습
- Value Iteration
- markov decision process
- 결합 엔트로피
- policy iteration
- markov reward process
- 바닥부터 배우는 강화학습
- 벨만최적방정식
- n-step TD
- 조건부 엔트로피
- TD target
- 정보량
- gnn
- Temporal Difference
- linear combination
- 마르코프 프로세스
- linearly independent
- markov process
- 벨만방정식
- Today
- Total
Jaehoon Jung
(3) Bellman Equation 본문
※ MDP ≡ (S,A,P,R,γ)(S,A,P,R,γ)가 주어졌을 때, 우리가 풀고자 하는 문제는 2가지 종류가 있다.
(1) Prediction - 특정한 policy ππ가 주어졌을 때, 각 state의 value를 평가하는 문제
(2) Control - optimal policy π∗π∗를 찾는 문제
→→ optimal policy π∗π∗를 따를 때의 value function을 optimal value function v∗v∗라고 부른다.
※ 우리의 목적은 MDP의 optimal policy π∗π∗와 optimal value function v∗v∗을 찾아내어 MDP를 푸는 것이다.
※ 대부분의 강화학습 알고리즘은 value를 구하는 것에서 출발하며, Bellman Equation을 기반으로 value를 구한다.
- Bellman Equation은 t 시점에서의 value와 t+1 시점에서의 value 사이의 관계, value function과 policy function 사이의 관계를 다루고 있으며, Bellman Expectation Equation 과 Bellman Optimality Equation이 있다.
(1) Bellman Expectation Equation
- Bellman Expectation Equation은 현재 state의 value와 next state의 value 사이의 관계를 나타내고 있다.

→→ 만약 value function이 참 값이라면 등호가 성립하겠지만, 그렇지 않다면 우항과 좌항의 값이 다르다!
→→ Eπ[rt+1+γvπ(st+1)]Eπ[rt+1+γvπ(st+1)]의 값으로 원래 value function의 값을 Update해나간다. 이 과정을 많이 진행하다보면 True value function에 값이 수렴하게 되고, 이는 주어진 policy ππ에 대한 True value function을 찾은 것이다.

→→ 위와 동일하게 Q-function(= state-action value function)에 대해서도 Bellman Expectation Equation을 구할 수 있다.
※ 위의 Bellman Expectation Equation은 next state의 value 값의 기대값으로 표현되어 있어 바로 계산하기 어렵다는 문제가 있다. 이를 policy 와 transition probability로 표현하여 실제로 계산할 수 있게된다!!
1단계) qπ(s,a)qπ(s,a)를 이용해 vπ(s)vπ(s) 계산하기 && vπ(s)vπ(s)를 이용해 qπ(s,a)qπ(s,a) 계산하기
(1) qπ(s,a)qπ(s,a)를 이용해 vπ(s)vπ(s) 계산하기
- 현재 state s에서 가능한 모든 action에 대해서 policy function과 action value function의 곱을 모두 더한 것으로 현재 state s의 value를 나타낼 수 있다.

(2) vπ(s)vπ(s)를 이용해 qπ(s,a)qπ(s,a) 계산하기
- 현재 state s에서 특정 action을 취했을 때 받게 되는 reward + 해당 action으로 갈 수 있는 모든 next state에 대해서 next state로 이동할 확률 x next state의 value function의 합으로 Q-function을 나타낼 수 있다.

2단계) 1단계의 식을 기존의 Bellman Expectation Equation 식에 대입하여 계산가능한 Bellman Expectation Equation 만들기

※ 2단계의 계산가능한 Bellman Expectation Equation을 계산하기 위해서는 아래 2가지를 반드시 알고 있어야한다.
(1) reward function rasras - 각 state에서 action a를 취했을 때 받게되는 reward
(2) Transition probability Pass′ - 각 state에서 action a를 취했을 때 이동할 수 있는 next state의 확률분포
※ reward function과 Transition probability는 Environment의 일부이며, 이 2가지 정보를 알고 있을 때, "MDP를 알고있다"라고 표현한다! 여기서, reward function을 안다는 것은 state s에서 action a를 해보기도 전에 expected reward의 값을 안다는 것이며, Transition probability을 안다는 것은 state s에서 action a를 했을 때 어떤 next state로 이동할지에 대한 확률분포를 미리 알고 있다는 것을 의미한다.
1) Model-based (Planning) 접근법 - MDP에 대한 정보를 알고 학습하는 접근법 (2단계 Bellman Expectation Equation 사용!)
2) Model-free 접근법 - MDP에 대한 정보를 모를 때 학습하는 접근법 (0 단계 Bellman Expectation Equation 사용!)
(2) Optimal policy & Optimal value
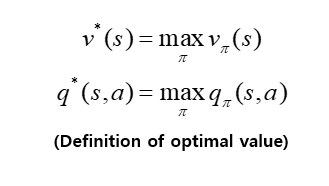
→ optimal value는 어떤 MDP가 주어졌을 때, 그 MDP안에 존재하는 모든 policy π들 중에서 value의 갚을 가장 높게하는 π를 선택하여 계산한 value를 의미한다.
※ optimal policy π∗는 모든 state에 대해서 어떤 policy π보다 높은 value를 얻도록하는 policy를 의미한다. 즉, 모든 policy들 중에서 가장 좋은 policy를 의미한다.
→ optimal policy π∗가 정의되면 아래와 같은 등식이 성립한다.

(3) Bellman Optimality Equation
- Bellman Optimality Equation은 optimal value !! v^*(s)와q^*(s,a)!!에 대한 수식이다.
→ Bellman Expectation Equation에서는 policy에 의해 특정 action을 선택하는 확률, 선택된 action에 의해 next state로 이동할 확률과 같이 확률적인 요소로 인해 Expectation연산자가 사용되었지만, Bellman optimality Equation에서는 action을 확률적으로 취하지 않고, 가장 좋은 action을 max연산자로 취하기 때문에 policy에 의한 확률적인 요소가 사라진다.

→ 모든 action들 중에서 E[r+γv∗(s′)]의 값을 가장크게 하는 action a를 선택한다.

※ 위의 Bellman Optimality Equation도 next state의 value 값의 기대값으로 표현되어 있어 바로 계산하기 어렵다는 문제가 있다.
1단계) q∗를 이용해 v∗ 계산하기 && v∗를 이용해 q∗ 계산하기
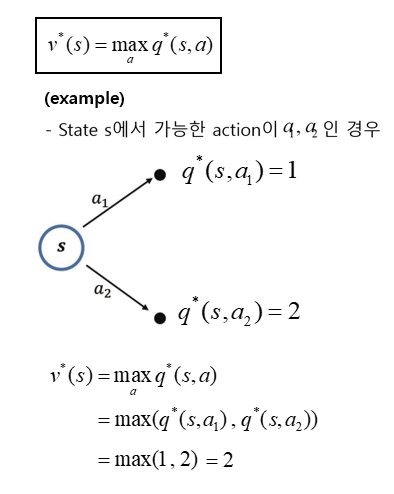
(1) q∗를 이용해 v∗ 계산하기
- state s의 optimal value는 s에서 선택할 수 있는 action들 중 value가 가장 높은 action value와 동일하다.
(2) v∗를 이용해 q∗ 계산하기

2단계) 1단계의 식을 기존의 Bellman Optimality Equation 식에 대입하여 계산가능한 Bellman Optimality Equation 만들기

※ (1) 특정 policy π가 주어져 있고, π를 평가하고 싶을 때 Bellman Expectation Equation을 사용한다.
(2) Optimal value를 찾는 일을 할 때 Bellman Optimality Equation을 사용한다.
Reference) "바닥부터 배우는 강화학습 by 노승은"
'AI > 강화학습' 카테고리의 다른 글
| (4) Policy Iteration & Value Iteration (0) | 2022.10.22 |
|---|---|
| (2) Markov Decision Process (MDP) (0) | 2022.10.20 |
| (1) 강화학습 (0) | 2022.10.20 |



